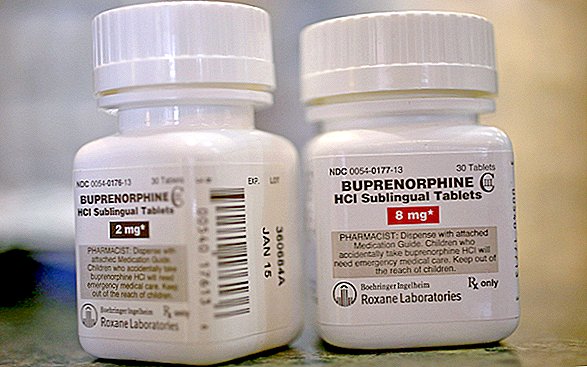
Subtitrare: vedere asupra lunii la perigeiu și apogeu
În calitate de profesor, sunt mereu în căutarea laboratoarelor cu setări simple potrivite elevilor. Favoritul meu actual este găsirea vitezei luminii cu ciocolata.
Într-o nouă lucrare încărcată recent pe arXiv, Kevin Krisciunas din Texas A&M descrie o metodă pentru a determina excentricitatea orbitală a lunii, cu o eroare surprinzător de scăzută, folosind nimic mai mult decât un stick de metru, o bucată de carton și un program destinat pentru montarea curbelor la stele variabile.
Această metodă folosește faptul că excentricitatea poate fi determinată din raportul dintre mărimea unghiulară medie a unui obiect și jumătate din amplitudinea sa. Astfel, obiectivul principal este măsurarea acestor două cantități.
Strategia lui Kevin pentru a face acest lucru este de a folosi un orificiu de observare a cartonului care poate aluneca de-a lungul unui stick de metru. Privind prin gaura de la lună și glisând cartea înainte și înapoi până când dimensiunea unghiulară a găurii doar se suprapune lunii. De acolo, diametrul orificiului împărțit la distanța în jos a barei contorului dă dimensiunea unghiulară datorită formulei unghiului mic (? = D / D la radieni dacă D >> d).
Pentru a preveni erorile sistematice în judecarea greșită, deoarece cardul este alunecat înainte până când dimensiunea găurii se potrivește cu luna, cel mai bine este să o abordați și din cealaltă direcție; Venind de la capătul îndepărtat al bățului contorului. Acest lucru ar trebui să contribuie la reducerea erorilor și în încercarea lui Kevin, el a descoperit că a avut o răspândire tipică de ± 4 mm atunci când a făcut acest lucru.
În acest moment, există încă o altă eroare sistematică care trebuie luată în considerare: elevul are o dimensiune fină comparabilă cu orificiul de observare. Acest lucru va determina subestimarea dimensiunii unghiulare reale. Ca atare, este necesar un factor de corecție.
Pentru a obține acest factor de corecție, Kevin a plasat un disc de 91 mm la o distanță de 10 metri (acest lucru ar trebui să producă un disc cu aceeași dimensiune unghiulară ca luna atunci când este privit de la distanță). Pentru a produce cea mai bună potrivire, alunecarea de carton cu gaura de observare ar trebui să trebuie să fie plasat la 681,3 mm pe batonul contorului, dar din cauza erorii sistematice a elevului, Kevin a considerat că trebuie să fie plasat la 821 mm. Raportul dintre plasarea observată și plasarea corespunzătoare a furnizat factorul de corecție pe care Kevin l-a folosit (1.205). Acest lucru ar trebui să fie calibrat pentru fiecare persoană în parte și ar depinde, de asemenea, de cantitatea de lumină în timpul observației, deoarece acest lucru afectează și diametrul elevului. Cu toate acestea, adoptarea unui singur factor de corecție produce rezultate satisfăcătoare.
Aceasta permite date luate în mod corespunzător, care pot fi apoi utilizate pentru a determina cantitățile necesare (dimensiunea unghiulară medie și 1/2 amplitudinea). Pentru a determina acestea, Kevin a folosit un program cunoscut sub numele de PERDET, care este conceput pentru montarea curbelor sinusoidale la oscilațiile stelelor variabile. Aveți vreun program care să poată adapta astfel de curbe la punctele de date folosind un?2 potrivite sau o analiză Fourier ar fi potrivită în acest scop.
Din astfel de programe, odată determinată dimensiunea unghiulară medie și jumătate de amplitudine, raportul lor asigură excentricitatea. Pentru experimentul lui Kevin, el a găsit o valoare de 0,039 ± 0,006. În plus, perioada pe care a determinat-o de la perigeu la perigeu a fost de 27,24 ± 0,29 zile, ceea ce este de acord excelent cu valoarea acceptată de 27,55 zile.